integration by parts Archives | Jake's Math Lessons

Cylinder/Shell Method – Rotate around a horizontal line

Before reading through this problem, I’d recommend checking out my lesson on finding volumes of rotation using the cylinder shell method. I’m not going to go into quite as much detail here as I did in that lesson. It might help you make more sense of what’s going on if your start there.

Other than that there isn’t much else to add so let’s jump into an example!

Example 1

Find the area of the solid created by rotating the area bounded between $y= (x-1)^3-3$ , $y=-x-2$ , and $y=-2$ about the line $y=-1$ .

Just as before I’ll use the same 4 step process as in the cylinder method lesson.

1. Graph the 2-D functions

As I always say, I suggest starting any problem possible by drawing what is being described to you. Go ahead and start with graphing all of the functions described in the problem. I’ll do this using Desmos. You should end up with something like the graph below. I also went ahead and shaded the bounded region gray to make it a little easier to see (this was not done in Desmos).

$y= (x-1)^3-3$ , $y=-x-2$ , $y=-2$ , and $y=-1$

$y= (x-1)^3-3$ , $y=-x-2$ , $y=-2$ , and $y=-1$

2. Rotate the 2-D area around the given axis

Again, we want to visualize what the question is asking us to find. We will need to take the shaded region in the above graph and rotate it around the line $y=-1$ . Doing this would create a 3-D figure whose volume we’ll need to find. But first let’s draw it.

To do this, imagine the 2-D gray region coming off the paper or screen and rotating around the axis of rotation. Doing this would give us something like the figure below.

Figure resulting from rotating the area around a horizontal. — Result of rotating the region about the line $y=-1$ .

Result of rotating the region about the line $y=-1$ .

3. Setting up the integral

I’m not going to go into as much detail to explain where this integral comes from as I did in the cylinder method lesson, but if the following integral confuses you I’d recommend checking that lesson out by clicking on the above link.

Long story short, we want to imagine our 3-D figure is made up of several infinitely thin cylindrical shells. Adding up the volume of all of these shells would result in an integral like this: $$\int 2 \pi r h \ dr.$$

In order to help with coming up with each of these pieces, we need to relate them back to our figure and the functions that created it. In order to visualize this, let’s draw our figure with one of these infinitely thin shells that make up the entire figure. We can consider this one shell and how to represent these dimensions in terms of the given functions.

You can see one of these cylindrical shells represented in the drawing below with a labeled version of the cylinder draw in the upper-right hand corner.

3-D figure with a cylindrical shell — 3-D figure with a sample cylindrical shell shown in green.

As with all cylinder shell method problems, we need to imagine integrating from the center of the cylinder out to the outer edge. Since our cylinder is laying horizontally, moving from its center to its edge moves up and down. This means we are moving in the y direction. Therefore, we need to integrate in the y direction and represent our integral only in terms of y (we shouldn’t have any x‘s).

So let’s think about each of the three pieces that make up our integral one at a time.

Finding r

The radius of this cylinder would simply be the distance between the center of the cylinder and the edge. You can see in the smaller version of the cylinder drawn off to the side that the radius is represented by the red line measuring between the points labeled $(x_2, \ -1)$ and $(x_2, \ y)$ .

Since these two points have the same x value, we can find the distance between them by simply finding the distance between their y values. To do this we just need to take the larger value and subtract the smaller one from it. $$r=-1-y$$

Finding h

The height of a cylinder will always be measured as the distance between the two flat, parallel faces. Usually they would be the top and bottom, but since our cylinder is sideways, we need the distance between the left side and right side.

Looking at the smaller cylindrical shell off to the side in the drawing above, you can see the height of this cylinder is represented by the red line measuring the distance between the points $(x_1, \ y)$ and $(x_2, \ y)$ .

Similar to what we did before, these two points have the same y value. As a result, the distance between them would be the same as the distance between their x values. So we just need to take the larger x value and subtract away the smaller one. $$h=x_2-x_1$$

But remember earlier I said we need everything just in terms of y?

So we need to think about how we can rewrite $x_1$ and $x_2$ in terms of y.

Finding 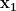$\mathbf{x_1}$

We know that $x_1$ lies on the function $y=-x-2$ so we know that the relationship between $x_1$ and y can be described in the same way $$y=-x_1-2.$$ If we rearrange this to solve for $x_1$ instead of y, we can use this to replace the $\mathbf{x_1}$ in our equation for h. $$y=-x_1-2$$ $$y+x_1=-2$$ $$x_1=-y-2$$

We can use this to rewrite h but replace the $x_1$ with $(-y-2)$ since we know they are equal. $$h= \ x_2- (-y-2)$$ Now we need to do the same thing with $x_2$ .

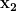
Finding $\mathbf{x_2}$

We are going to apply the same idea here as in the previous section. We know that $x_2$ lies on the function $y= (x-1)^3-3$ . Therefore, we can describe the relationship between $x_2$ and y as $$y= (x_2-1)^3-3.$$ Now we can solve this equation for $x_2$ and plug this into our equation for h. $$y \ = \ (x_2-1)^3-3$$ $$y+3 \ = \ (x_2-1)^3$$ $$\sqrt[3] {y+3} \ = \ x_2-1$$ $$\sqrt[3] {y+3} +1 \ = \ x_2$$ Now going back to our equation for h, this tells us $$h \ = \ \sqrt[3] {y+3} +1 – (-y-2).$$ And to simplify a bit: $$h \ = \ \sqrt[3] {y+3} +1 + y+2$$ $$h \ = \ \sqrt[3] {y+3} + y+3.$$ Now that we have h and r, we just need to find dr.

Finding dr

This is actually the simplest part to find. The dr represents the change in the cylinder’s radius as we go from each shell to the next. Since we move in the same direction of the radius as we integrate to find our volume, the change in r should be the same as the change in y between each step. Therefore, we can say that $$dr=dy.$$

Putting it all back into an integral

We already figured out that the volume of our figure can be found by using the integral $$\int 2 \pi rh \ dr.$$ And we just found these three pieces to be $$r=-1-y$$ $$h \ = \ \sqrt[3] {y+3} + y+3$$ $$dr=dy.$$ So we can just plug them into our integral. $$ \int 2 \pi \ ( -1-y ) \ \Big( \sqrt[3] {y+3} + y+3 \Big) \ dy$$

Now we need one last piece. We need to add bounds on the integrals.

Since we are integrating with respect to y, the bounds of our integrals need to be the range of y values that make up our original 2-D area. Looking back at our original graph, we can see that the original area bounded by the given functions spans over all of the y values between $y=-2$ and $y=-3$ . Therefore, we know that the volume of our figure will be $$V \ = \int_{-3}^{-2} 2 \pi \ ( -1-y ) \ \Big( \sqrt[3] {y+3} + y+3 \Big) \ dy.$$

4. Solve the integral

Now all we need to do is solve the integral we just found and that will leave us with our volume. This is actually a pretty complicated integral as is it, so let’s start with simplifying it a bit. We’ll do this by pulling out the constant, distributing out through the parenthesis, and combining like terms.

$$V \ = \int_{-3}^{-2} 2 \pi \ ( -1-y ) \ \Big( \sqrt[3] {y+3} + y+3 \Big) \ dy$$ $$V \ = \ 2 \pi \int_{-3}^{-2} \ – \big(y+3 \big)^{\frac{1}{3}} – y \ – 3 -y \big(y+3 \big)^{\frac{1}{3}} – y^2 – 3y \ \ dy$$ $$V \ = \ 2 \pi \int_{-3}^{-2} \ – \big(y+3 \big)^{\frac{1}{3}} -y \big(y+3 \big)^{\frac{1}{3}} – y^2 – 4y -3 \ \ dy$$

Now that we have it in a form that is simplest to integrate we can go ahead and integrate this function one term at a time. I’m not going to show every step of how to do this, but if you’d like to work it out on your own, I’d suggest using u-substitution on the $-(y+3)^{1/3}$ term and using integration by parts on the $-y(y+3)^{1/3}$ term.

$$V \ = \ 2 \pi \Bigg[ – \frac{3}{14} \big( y+3 \big)^{\frac{4}{3}}\big( 2y-1 \big) – \frac{1}{3}y^3 – 2y^2 – 3y \Bigg]_{-3}^{-2}$$

Again, I’m not going to show every step of this. Instead I used Wolfram Alpha from here, but if you evaluate this expression from $y=-3$ to $y=-2$ , you’ll see that $$V \ = \ 2 \pi \bigg(\frac{73}{42} \bigg)$$ $$V \ = \ \frac{73 \pi}{21}$$

Hopefully all of this helps you gain a bit of a better understanding of this method, but as always I’d love to hear your questions if you have any. Just email me at jakesmathlessons@gmail.com and I’ll see if I can help provide a bit more clarification. You can also use the form below to subscribe to my email list and I’ll send you my bonus FREE calc 1 study guide! Just put in your name and email address and I’ll be sure to let you know when I post new content! Feel free to go check out my other lessons and solutions about integrals as well.

Integration by parts practice problems

In a previous lesson, I explained the integration by parts formula and how to use it. Sometimes though, finding an integral using integration by parts isn’t as simple as the problem I did in that lesson. So I’d like to show some other more complex cases and how to work through them.

$\mathbf{1. \ \int 4x^2 \ sin(5x) \ dx}$ – Solution

$\mathbf{2. \ \int xe^{-2x} \ dx}$ – Solution

$\mathbf{3. \ \int x^{\frac{3}{2}}ln(x) \ dx}$ – Solution

Example 1

Evaluate the integral $$\int 4x^2 \ sin(5x) \ dx.$$

I will proceed through this problem following the same steps that I used in the integration by parts lesson.

1. Picking u and dv

Remember, we want to pick the piece of our function that we’d rather differentiate to be u, and the piece we’d rather integrate to be dv. The integral we need to evaluate can clearly be thought of as the product of $4x^2$ and $sin(5x)$ . Therefore, we need to take the derivative of one of these and the anti-derivative of the other.

First consider the $4x^2$ piece. If we take the derivative of this function we’ll end up with an x term, but if we take the anti-derivative we’ll end up with an $x^3$ term. This is due to the power rule. Generally it’s best to choose whichever will result in the simplest option. When it comes to polynomials, the simpler one is whichever has the lower power. Therefore, it is preferred to take the derivative of the $4x^2$ piece because the x term resulting from the derivative is simpler than the $\mathbf{x^3}$ term resulting from taking the anti-derivative.

But before we say that we definitely want to assign the $4x^2$ to be u so that we can take its derivative, we want to think about what this will mean for the sin(5x) piece.

What we need to consider is the difference between taking the derivative and the anti-derivative of sin(5x). In either case, we will end up with some constant multiplied by cos(5x) (we can find this using the chain rule for the derivative or u-substitution for the anti-derivative). But you can see that the derivative and the anti-derivative of this piece are equally complex, so it doesn’t make much of a difference whether we say the sin(5x) piece is assigned to u or dv.

Since the derivative of $4x^2$ is much simpler than its anti-derivative, we would rather call it u than dv. And it doesn’t make a difference if sin(5x) is considered to be u or dv. So we will say $$u=4x^2$$ $$dv=sin(5x) \ dx.$$

2. Finding v and du

Now to find v we simply need to take the anti-derivative of the dv piece from the previous section. And to find du we need to take the derivative of u.

You can find the anti-derivative of sin(5x) by using u-substitution. I’m not going to show all the steps for this, but we will need to use the fact that the anti-derivative of sin(x) is -cos(x). Knowing this, we can find that the anti-derivative of sin(5x) would give us $$v=- \ \frac{1}{5} cos(5x).$$

Now that we have found v, let’s move onto finding du. This can simply be done by finding the derivative of u from part 1. Finding the derivative of $4x^2$ can simply be found using the power rule. Doing this gives us $$du=8x \ dx.$$

3. Plugging it all into the formula

Now that we have found all 4 of the pieces we need, we just have to plug them into the integration by parts formula. To summarize, the 4 pieces we have up to this point are $$u=4x^2$$ $$dv=sin(5x) \ dx$$ $$v=- \ \frac{1}{5} cos(5x)$$ $$du=8x \ dx.$$

So we just need to use the integration by parts formula with these. $$\int u \ dv = uv – \int v \ du$$ $$\int 4x^2 \ sin(5x) \ dx = \Big(4x^2\Big) \bigg(- \ \frac{1}{5} cos(5x) \bigg) – \int – \ \frac{1}{5} cos(5x) \ 8x \ dx$$

Now we can simplify and evaluate the integral on the right side of our equation. $$(1): \ \int 4x^2 \ sin(5x) \ dx = \ – \ \frac{4}{5} x^2 \ cos(5x) \ + \ \frac{8}{5}\int x \ cos(5x) \ dx$$

But notice, the integral on the right side of our equation is still fairly complex. We still have an integral which is the product of two simpler functions, x and cos(5x). In order to evaluate this integral we’ll actually need to use integration by parts again. So now we need to use integration by parts to evaluate $$\int x \ cos(5x) \ dx.$$ We’ll go ahead and follow the same steps as we did before, but now we have a new integral and will need to reassign our u and dv.

4. Picking u and dv

Now that we are going through this process a second time, we don’t really have much of a choice when we pick which piece will be u and dv. The reason for this is that we will need to make this determination based on what we did the first time through. Consider where each of our pieces came from. One of our pieces is x, which came from the $4x^2$ in our original integral. And the other piece is cos(5x) which came from the sin(5x) in the original integral.

Since the x piece in our current integral came from the $4x^2$ piece in the original integral, and we decided that the $4x^2$ piece would be u earlier, we need to follow up by doing the same here. Therefore, we will say $$u=x$$ this time around.

By the same reasoning, we will need to say that $$dv = cos(5x) \ dx$$ this time around since we said assigned the sin(5x) to dv the first time through.

5. Finding v and du

Now we just need to take the u and dv from the previous step and use them to find v and du.

To find v we just need to find the anti-derivative of dv. We previously decided that $dv = cos(5x) \ dx$ . Just like before, we can find this anti-derivative using u-substitution. Doing this tells us that $$v = \frac{1}{5} sin(5x).$$

And now we just need to find du by taking the derivative of u. Since we know $u = x$ , we know that $$du=dx.$$

6. Plugging it all into the formula

And finally we just need to plug the 4 pieces we have found into the integration by parts formula. So far we have found $$u=x$$ $$dv = cos(5x) \ dx$$ $$v = \frac{1}{5} sin(5x)$$ $$du=dx.$$

Now putting these into the integration by parts formula we find $$\int u \ dv = uv – \int v \ du$$ $$\int x \ cos(5x) \ dx \ = \ x \bigg( \frac{1}{5} sin(5x) \bigg) \ – \int \frac{1}{5} sin(5x) \ dx$$ $$\int x \ cos(5x) \ dx \ = \ \frac{1}{5} x \ sin(5x) \ – \ \frac{1}{5} \int sin(5x) \ dx$$

And now the integral we need to evaluate is much simpler than what we started with. $$\int x \ cos(5x) \ dx \ = \ \frac{1}{5} x \ sin(5x) \ – \ \frac{1}{5} \bigg( – \frac{1}{5} cos(5x) \bigg)$$ $$\int x \ cos(5x) \ dx \ = \ \frac{1}{5} x \ sin(5x) \ + \ \frac{1}{25} cos(5x)$$

Wrapping it all together

Now that we have found $$\int x \ cos(5x) \ dx \ = \ \frac{1}{5} x \ sin(5x) \ + \ \frac{1}{25} cos(5x)$$ we can bring this back to our equation (1) back in step 3. And all we need to do is replace the $\int x \ cos(5x) \ dx$ with $\frac{1}{5} x \ sin(5x) \ + \ \frac{1}{25} cos(5x)$ . Doing this tells us that $$\int 4x^2 \ sin(5x) \ dx = \ – \ \frac{4}{5} x^2 \ cos(5x) \ + \ \frac{8}{5}\int x \ cos(5x) \ dx$$ $$= \ – \ \frac{4}{5} x^2 \ cos(5x) \ + \ \frac{8}{5} \bigg( \frac{1}{5} x \ sin(5x) \ + \ \frac{1}{25} cos(5x) \bigg)$$ $$= \ – \ \frac{4}{5} x^2 \ cos(5x) \ + \ \frac{8}{25} x \ sin(5x) \ + \ \frac{8}{125} cos(5x)$$

And that’s our answer! Clearly a bit more complicated than the first integration by parts example I did, but it isn’t too bad. You essentially just need to apply the same process two time in a row. As long as you stay consistent in your designations of u and dv each time, it should all work out in the end.

Example 2

$$\int xe^{-2x} \ dx$$

We’ll start this by deciding which piece we’ll call u and which piece is dv.

$$u=x$$ $$dv=e^{-2x} \ dx$$

Then we need to use these to figure out du and v.

$$du=1 \cdot dx=dx$$ $$v=-\frac{1}{2}e^{-2x}$$

Now we can plug all 4 of these pieces into the integration by parts formula.

$$\int xe^{-2x} \ dx \ = \ x \bigg( -\frac{1}{2}e^{-2x} \bigg) – \int -\frac{1}{2}e^{-2x} \ dx$$

At this point we are left with a simpler integral to evaluate.

$$= -\frac{1}{2}xe^{-2x} + \frac{1}{2} \int e^{-2x} \ dx$$ $$= -\frac{1}{2}xe^{-2x} + \frac{1}{2} \bigg( -\frac{1}{2} e^{-2x} \bigg)$$ $$= -\frac{1}{2}xe^{-2x} – \frac{1}{4} e^{-2x}$$ $$= -\frac{1}{2}e^{-2x} \bigg( x + \frac{1}{2} \bigg)$$

Example 3

$$\int x^{\frac{3}{2}}ln(x) \ dx$$

We’ll start this by deciding which piece we’ll call u and which piece is dv.

$$u=ln(x)$$ $$dv=x^{\frac{3}{2}} \ dx$$

Then we need to use these to figure out du and v.

$$du=\frac{1}{x} \ dx$$ $$v=\frac{2}{5}x^{\frac{5}{2}}$$

Now we can plug all 4 of these pieces into the integration by parts formula.

$$\int x^{\frac{3}{2}}ln(x) \ dx \ = \ \frac{2}{5}x^{\frac{5}{2}} ln(x) \ – \int \frac{1}{x} \cdot \frac{2}{5}x^{\frac{5}{2}} \ dx$$

At this point we are left with a simpler integral to evaluate.

$$= \ \frac{2}{5}x^{\frac{5}{2}} ln(x) \ – \ \frac{2}{5} \int x^{\frac{3}{2}} \ dx$$ $$= \ \frac{2}{5}x^{\frac{5}{2}} ln(x) \ – \ \frac{2}{5} \cdot \frac{2}{5} x^{\frac{5}{2}}$$ $$= \ \frac{2}{5}x^{\frac{5}{2}} \bigg( ln(x) \ – \ \frac{2}{5} \bigg)$$

As always, let me know if you have any questions. If anything was confusing here leave a comment or send me an email at jakesmathlessons@gmail.com and I’ll get back to you with an answer. You can also use the contact form below to reach out and I’ll send you my FREE calculus 1 study guide as a bonus! Also check out my other lessons about integrals!

Integration by parts

Integration by parts is another common technique used to find complex antiderivatives. This method tends to be a little more straight forward in its application than u-substitution. The main reason for this is that it requires the use of a formula, and if you can follow the formula you should be able to work through the rest.

First let’s introduce the formula, then I’ll explain how to use it. If you already know how to do these and you’re looking for extra practice problems, click here.

$$\int u \ dv = uv- \int v \ du$$

All this formula is really saying is that if we need to integrate some function which can be thought of as the product of two pieces, u and dv, then we can rewrite our integral in this other form. Notice we still would have an integral to solve after using this formula. But the hope is that $\int v \ du$ is easier to find than $\int u \ dv$ .

But how do you use the formula?

Using the integration by parts formula can be broken down into 3 simple steps and is going to start out somewhat similarly to integrating with u-substitution.