Tag: rotate

Cylinder/Shell Method – Rotate around a horizontal line

Before reading through this problem, I’d recommend checking out my lesson on finding volumes of rotation using the cylinder shell method. I’m not going to go into quite as much detail here as I did in that lesson. It might help you make more sense of what’s going on if your start there.

Other than that there isn’t much else to add so let’s jump into an example!

Example 1

Find the area of the solid created by rotating the area bounded between y= (x-1)^3-3, y=-x-2, and y=-2 about the line y=-1.

Just as before I’ll use the same 4 step process as in the cylinder method lesson.

1. Graph the 2-D functions

As I always say, I suggest starting any problem possible by drawing what is being described to you. Go ahead and start with graphing all of the functions described in the problem. I’ll do this using Desmos. You should end up with something like the graph below. I also went ahead and shaded the bounded region gray to make it a little easier to see (this was not done in Desmos).

y= (x-1)^3-3, y=-x-2, y=-2, and y=-1

2. Rotate the 2-D area around the given axis

Again, we want to visualize what the question is asking us to find. We will need to take the shaded region in the above graph and rotate it around the line y=-1. Doing this would create a 3-D figure whose volume we’ll need to find. But first let’s draw it.

To do this, imagine the 2-D gray region coming off the paper or screen and rotating around the axis of rotation. Doing this would give us something like the figure below.

Figure resulting from rotating the area around a horizontal.
Result of rotating the region about the line y=-1.

3. Setting up the integral

I’m not going to go into as much detail to explain where this integral comes from as I did in the cylinder method lesson, but if the following integral confuses you I’d recommend checking that lesson out by clicking on the above link.

Long story short, we want to imagine our 3-D figure is made up of several infinitely thin cylindrical shells. Adding up the volume of all of these shells would result in an integral like this: $$\int 2 \pi r h \ dr.$$

In order to help with coming up with each of these pieces, we need to relate them back to our figure and the functions that created it. In order to visualize this, let’s draw our figure with one of these infinitely thin shells that make up the entire figure. We can consider this one shell and how to represent these dimensions in terms of the given functions.

You can see one of these cylindrical shells represented in the drawing below with a labeled version of the cylinder draw in the upper-right hand corner.

3-D figure with a cylindrical shell
3-D figure with a sample cylindrical shell shown in green.

As with all cylinder shell method problems, we need to imagine integrating from the center of the cylinder out to the outer edge. Since our cylinder is laying horizontally, moving from its center to its edge moves up and down. This means we are moving in the y direction. Therefore, we need to integrate in the y direction and represent our integral only in terms of y (we shouldn’t have any x‘s).

So let’s think about each of the three pieces that make up our integral one at a time.

Finding r

The radius of this cylinder would simply be the distance between the center of the cylinder and the edge. You can see in the smaller version of the cylinder drawn off to the side that the radius is represented by the red line measuring between the points labeled (x_2, \ -1) and (x_2, \ y).

Since these two points have the same x value, we can find the distance between them by simply finding the distance between their y values. To do this we just need to take the larger value and subtract the smaller one from it. $$r=-1-y$$

Finding h

The height of a cylinder will always be measured as the distance between the two flat, parallel faces. Usually they would be the top and bottom, but since our cylinder is sideways, we need the distance between the left side and right side.

Looking at the smaller cylindrical shell off to the side in the drawing above, you can see the height of this cylinder is represented by the red line measuring the distance between the points (x_1, \ y) and (x_2, \ y).

Similar to what we did before, these two points have the same y value. As a result, the distance between them would be the same as the distance between their x values. So we just need to take the larger x value and subtract away the smaller one. $$h=x_2-x_1$$

But remember earlier I said we need everything just in terms of y?

So we need to think about how we can rewrite x_1 and x_2 in terms of y.

Finding 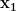\mathbf{x_1}

We know that x_1 lies on the function y=-x-2 so we know that the relationship between x_1 and y can be described in the same way $$y=-x_1-2.$$ If we rearrange this to solve for x_1 instead of y, we can use this to replace the \mathbf{x_1} in our equation for h. $$y=-x_1-2$$ $$y+x_1=-2$$ $$x_1=-y-2$$

We can use this to rewrite h but replace the x_1 with (-y-2) since we know they are equal. $$h= \ x_2- (-y-2)$$ Now we need to do the same thing with x_2.

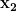
Finding \mathbf{x_2}

We are going to apply the same idea here as in the previous section. We know that x_2 lies on the function y= (x-1)^3-3. Therefore, we can describe the relationship between x_2 and y as $$y= (x_2-1)^3-3.$$ Now we can solve this equation for x_2 and plug this into our equation for h. $$y \ = \ (x_2-1)^3-3$$ $$y+3 \ = \ (x_2-1)^3$$ $$\sqrt[3] {y+3} \ = \ x_2-1$$ $$\sqrt[3] {y+3} +1 \ = \ x_2$$ Now going back to our equation for h, this tells us $$h \ = \ \sqrt[3] {y+3} +1 – (-y-2).$$ And to simplify a bit: $$h \ = \ \sqrt[3] {y+3} +1 + y+2$$ $$h \ = \ \sqrt[3] {y+3} + y+3.$$ Now that we have h and r, we just need to find dr.

Finding dr

This is actually the simplest part to find. The dr represents the change in the cylinder’s radius as we go from each shell to the next. Since we move in the same direction of the radius as we integrate to find our volume, the change in r should be the same as the change in y between each step. Therefore, we can say that $$dr=dy.$$

Putting it all back into an integral

We already figured out that the volume of our figure can be found by using the integral $$\int 2 \pi rh \ dr.$$ And we just found these three pieces to be $$r=-1-y$$ $$h \ = \ \sqrt[3] {y+3} + y+3$$ $$dr=dy.$$ So we can just plug them into our integral. $$ \int 2 \pi \ ( -1-y ) \ \Big( \sqrt[3] {y+3} + y+3 \Big) \ dy$$

Now we need one last piece. We need to add bounds on the integrals.

Since we are integrating with respect to y, the bounds of our integrals need to be the range of y values that make up our original 2-D area. Looking back at our original graph, we can see that the original area bounded by the given functions spans over all of the y values between y=-2 and y=-3. Therefore, we know that the volume of our figure will be $$V \ = \int_{-3}^{-2} 2 \pi \ ( -1-y ) \ \Big( \sqrt[3] {y+3} + y+3 \Big) \ dy.$$

4. Solve the integral

Now all we need to do is solve the integral we just found and that will leave us with our volume. This is actually a pretty complicated integral as is it, so let’s start with simplifying it a bit. We’ll do this by pulling out the constant, distributing out through the parenthesis, and combining like terms.

$$V \ = \int_{-3}^{-2} 2 \pi \ ( -1-y ) \ \Big( \sqrt[3] {y+3} + y+3 \Big) \ dy$$ $$V \ = \ 2 \pi \int_{-3}^{-2} \ – \big(y+3 \big)^{\frac{1}{3}} – y \ – 3 -y \big(y+3 \big)^{\frac{1}{3}} – y^2 – 3y \ \ dy$$ $$V \ = \ 2 \pi \int_{-3}^{-2} \ – \big(y+3 \big)^{\frac{1}{3}} -y \big(y+3 \big)^{\frac{1}{3}} – y^2 – 4y -3 \ \ dy$$

Now that we have it in a form that is simplest to integrate we can go ahead and integrate this function one term at a time. I’m not going to show every step of how to do this, but if you’d like to work it out on your own, I’d suggest using u-substitution on the -(y+3)^{1/3} term and using integration by parts on the -y(y+3)^{1/3} term.

$$V \ = \ 2 \pi \Bigg[ – \frac{3}{14} \big( y+3 \big)^{\frac{4}{3}}\big( 2y-1 \big) – \frac{1}{3}y^3 – 2y^2 – 3y \Bigg]_{-3}^{-2}$$

Again, I’m not going to show every step of this. Instead I used Wolfram Alpha from here, but if you evaluate this expression from y=-3 to y=-2, you’ll see that $$V \ = \ 2 \pi \bigg(\frac{73}{42} \bigg)$$ $$V \ = \ \frac{73 \pi}{21}$$

Hopefully all of this helps you gain a bit of a better understanding of this method, but as always I’d love to hear your questions if you have any. Just email me at jakesmathlessons@gmail.com and I’ll see if I can help provide a bit more clarification. You can also use the form below to subscribe to my email list and I’ll send you my bonus FREE calc 1 study guide! Just put in your name and email address and I’ll be sure to let you know when I post new content! Feel free to go check out my other lessons and solutions about integrals as well.


Washer Method – Rotate around a vertical line

Find the volume obtained by rotating the region bounded by y=\frac{1}{4} x^2, x=2, and y=0 about the y-axis.

To solve this problem, I’m going to use the same 4 step process as I did in my disk method lesson and my first washer method practice problem. There is one key difference this time around: here we are rotating the region around a vertical line. Previously, I have only shown examples of rotating around a horizontal line.

1. Graph the 2-D functions

As I did in the other examples mentioned above, the first thing we should always do is graph the given functions. This will help us visualize what we’re dealing with and will make it easier to come up with the function we’ll need to integrate later.

All I will do here is plug these functions into Desmos, but see if you can graph these without the help of a calculator. That a skill that may come in handy at some point.

washer method around y axis
y=\frac{1}{4} x^2, x=2, and y=0

2. Rotate the 2-D area around the given axis

This is another step that is mostly helpful for visualization. Visualizing each step required to create the 3-D figure we’re looking for will make things a lot easier when we come up with the function that we need to integrate.

Remember, the problem said that we will need to rotate the region trapped between these three functions around the y-axis. So imagine this 2-D region rotating off the page (or screen) and around the y-axis. Doing this would create a round 3-D figure. This is the figure whose volume we need to find.

I encourage you to imagine this happening on your page and try drawing a rough sketch of the resulting figure. I will do this using Wolfram Alpha.

3D rotation around y axis
Result of rotating the region about the y-axis.

3. Setting up the integral

This step is at the heart of these problems. All of the graphing and sketching is to help us visualize what is being described so we can correctly formulate our integral.

We could solve this problem using the cylinder method as well, but that’s for another lesson. For this example, we will proceed using the washer method. This is important to distinguish here because we need to imagine all of the washers that make up this 3-D figure. What we need to think about is a stack of very, very, very thin washers stacked one on top of the other, in the same shape as the figure shown a couple paragraphs ago.

You will notice that if we imagine this figure as a stack of washers, the washers would be stacked vertically, one on top of the other. This is different from the first washer method example I did, where the washers were all side by side.

This is an important difference because adding up the volume of all of these washers will require us to move vertically throughout this figure to get the next washer and add its volume to the total. As a result of this, we will be integrating with respect to y! Since we move in the y direction to get to the next washer, we need to integrate with respect to y. Therefore, when we create our integral, it will all need to be in terms of y rather than x.

How do we set the integral up with respect to y?

Take a look at the drawing below. You can see one of these infinitely thin washers drawn in the figure. Let’s take a minute to consider the dimensions of this particular washer. Remember, as we showed in the first washer method practice problem, the volume of a washer is given by V=\pi h(R^2-r^2) where r is the inner radius and R is the outer radius.

labeled rotation around y axis

The large washer in the middle of our graph is there to help you visualize where these washers would be if we were to stack them up to create this figure. Take a look at the smaller washer in the upper left section of our graph. This will be used to help us find the inner and outer radii of the washers.

Finding the inner radius

The inner radius of a washer will be the distance between the center of the washer and the inner edge. In the drawing above, this is shown in the smaller washer off to the side as the distance between the points labeled (0, \ y) and (x, \ y).

(0, \ y) is some point on the y-axis. The y will be different depending on which washer we’re looking at, but since it lies on the y-axis we know that the x-coordinate will always be 0.

(x, \ y) is some point that lies on the function y=\frac{1}{4}x^2. But remember, I said earlier that we need to integrate with respect to y because our washers are stacked vertically so we move in the y direction to add up all of their volumes. Therefore, we need everything just in terms of y without having any x‘s around. So we need to rewrite (x, \ y) just in terms of y. In order to do this we will need to think about how we can write x in terms of y.

Since we know that this point lies on the function y=\frac{1}{4}x^2 we can use this relationship to find x in terms of y. All we need to do is take that equation and solve for x. $$y=\frac{1}{4}x^2$$ $$4y=x^2$$ $$\pm \sqrt{4y}=x$$ Notice, in general when we take the square root of both sides of the equation we need the positive and negative square root. In this case, the positive square root is the right half of the parabola and the negative square root represents the left half. Since the right half of the parabola is the part that formed the region we’re looking at, we only need the positive square root. So, $$x=\sqrt{4y}.$$

Now that we know x=\sqrt{4y} for any (x, \ y) pair that lies on our function, we can use this to say that (x, \ y) can instead be written as (\sqrt{4y}, \ y). Therefore, to find the inner radius we need to find the distance between \mathbf{(0, \ y)} and \mathbf{(\sqrt{4y}, \ y)}. To find this distance we simply need to find the difference between their x-values because they will always have the same y-coordinate. So, $$r= \sqrt{4y} \ – 0$$ $$r= \sqrt{4y}.$$

Finding the outer radius

Finding the outer radius will be very similar to finding the inner radius. The only difference is that we now need to find the distance between the point in the center of the washer and the outer edge. This is shown in the labeled washer by the distance between the two points labeled (0, \ y) and (2, \ y).

We know that any point that lies on the line x=2 will have an x-coordinate of 2. No matter what the y-coordinate is, if it lies on \mathbf{x=2} we know the x-coordinate must be 2. This is the reason why the point on the outer edge of the washer is labeled (2, \ y). Although the y-coordinate changes as we move up the side of our figure, the x-coordinate stays equal to 2.

So we need to find the distance between the points (0, \ y) and (2, \ y). Clearly these two points will have the same y-coordinate. The y-coordinate changes depending on which washer we are looking at in our figure, but these two points will have the same y-coordinate when they are on the same washer. Since they have the same y-value, to find the distance between them, we just need to find the distance between their x-coordinates. Therefore, $$R=2-0$$ $$R=2.$$

Finding the height (or thickness)

In order to find the volume of a washer we will also need it’s height.

The height of our infinitely thin washers is actually quite simple. Just like when we integrate a 2-D function to find the area under the curve, our slices here are all the same width. We don’t have to worry about each washer, having a different height.

The height of each washer will just be how far we always move over before taking another slice. Since we are moving up in the y direction as we imagine the next slice, this can simply be our change in y between the slices. Change in y is always represented as dy. So we can simply say the height of each cylinder is $$h=dy.$$

Back to the integral

Like I said before, all the integral will do is go through all the y values that our figure covers and add up the volumes of all of the infinitely thin washers. In order for it to achieve this, we need to put a function for the volume of each washer that depends on y. We already know that the volume of a washer in general would be $$V = \pi h \big( R^2 – r^2 \big).$$

This means that our integral might look something like this $$\int \pi h \big( R^2 – r^2 \big).$$

But this doesn’t really have any meaning on its own. In order to give this meaning we need to represent this volume in terms of y and give the integral a range of y values to integrate over.

Remember we also found the inner radius, outer radius, and height of the washers that make up our figure to be $$r=\sqrt{4y},$$ $$R=2,$$ $$h=dy.$$

Putting all of this into an integral along with the fact that this figure goes across all y-values between 0 and 1, give us $$V= \int_0^1 \pi (dy) \bigg( (2)^2 – \Big(\sqrt{4y}\Big)^2 \bigg).$$

Of course, this looks a little strange. Let’s simplify this integral and rearrange the pieces a bit. $$V= \pi \int_0^1 4 – 4y \ dy$$

4. Solve the integral

Now we’ve gotten through the hard part. All we need to do now is evaluate the volume integral by finding the anti-derivative and evaluating the bounds. All we need in this case is the power rule for integration. $$V= \pi \int_0^1 4 – 4y \ dy$$ $$V= \pi \bigg[ 4y – 2y^2 \bigg]_0^1$$ $$V= \pi \bigg[ \Big( 4(1) – 2(1)^2 \Big) – \Big( 4(0) – 2(0)^2 \Big) \bigg]$$ $$V=\pi(4-2)$$ $$V=2 \pi$$

So the volume of this solid is 2 \pi cubic units! I hope that helps, but if you are still looking for some practice with the washer method go check out my first washer method problem. That one explains the rational behind some of the steps in a bit more detail. You should also check out my other lessons and problems about integrals.

If you still have any questions, comments, or suggestions I’d love to hear them. Email me at jakesmathlessons@gmail.com or us the form below to submit your name and email and I’ll send you my calculus 1 study guide as a free gift!

Rotating Volumes with the Disk Method

Rotating functions around an axis to create a 3-D shape then finding its volume is one of the more common applications of integrals. This is commonly referred to as finding a volume using the disk method. It seems like a complicated type of problem, but if you think about what you are actually measuring it isn’t so bad.

Let’s think about a specific example. Imagine taking the function y=x^2 between x=0 and x=2 and rotating it around the x-axis then finding the volume of this solid using the disk method.

1. Graph the 2-D function

The first thing I would recommend doing with a problem like this is to graph the function that’s given to you. Here we are graphing y=x^2 within our given domain of 0 \leq x \leq 2. Using Wolfram Alpha we can see this graph below.

finding volumes with the disk method

2. Rotate the 2-D function around the given axis

Once you graph the function on the 2-D x-y-plane we need to imagine rotating it around the axis given in the problem. This will result in creating a 3-D figure whose volume we need to find.

In this case we need to rotate this portion of our function around the x-axis. Another way to say this is that we are rotating around the line y=0. Again, using Wolfram Alpha we can see what this figure would look like.

rotating function for disk method

I would always recommend drawing out the 2-D graph and 3-D rotation anytime you need to find the volume of a solid like this. It helps to visualize the solid whose volume you are trying to measure and it makes it much easier to make sure you are setting up your problem correctly.

3. Setting up the integral

As with any problem where we need to find a volume using the disk method, what we want to imagine here is having infinitely thin cylinders stacking up to create our 3-D figure. When we add up the volumes of all of these infinitely thin cylinders, get the volume of the entire figure. This is all the integral is doing.

disk method

You can see in this drawing our function has been rotated around the x-axis to create a round cone-like 3-D figure. The green cylinder in the figure represents one of the infinitely thin disks that we are slicing the figure into.

Since we are trying to make this integral represent the sum of all of these disks, we need to think about the volume of each disk in particular. Clearly each disk is a very thin cylinder. So in order to find their volumes, we should start with the volume of a cylinder, which is

$$V=\pi r^2 h.$$

Thinking back to our example of rotating y=x^2 around the x-axis, let’s determine the radius and height of our cylinders.

How do we find the radius?

Considering that each cylinder will be a different size, it seems clear that the radius of each cylinder will depend on which cylinder we’re considering. In fact, if you look at our drawing, you can see that the radius of each cylinder will simply depend on the x value where it’s sitting.


You can see in the drawing above that I drew a copy of the disk we are considering down below the function. Imagine we are trying to find the distance between the two points we labeled. The center point of our disk is labeled (x, 0). We know that the center of our disk will always have a y-coordinate of 0 because we rotated our function around the line \mathbf{y=0}. And we will leave the x-coordinate as the variable x because we are trying to find the volume of any disk along this figure with all different x values, not just the one disk drawn above.

Now consider the upper point. This point is labeled (x, y). This is just meant to be any (x, y) combination that sits on our function y=x^2. This point will always have the same x-value as our other labeled point, so the distance between these two points will simply be the distance between their y-coordinates, which are y and 0. To find the distance between these two values, we just need to do the larger value minus the smaller one, or y-0, which is just y.

But we need this to be in terms of x. Remember we realized earlier that the radius of our disk will depend on x, so we want everything in terms of x. We know that our point (x, y) we were looking at is some point that lies on our function. So we know \mathbf{y=x^2}. Therefore, if the radius of our disk is y, we can also say that the radius is x^2. So,

$$r=x^2.$$

How do we find the height?

The height of our infinitely thin cylinders is actually quite simple. Just like when we integrate a 2-D function to find the area under the curve, our slices here are all the same width. We don’t have to worry about each disk, or cylinder, having a different height.

The height of each cylinder will just be how far we always move over before taking another slice. Since we are moving over in the x direction as we imagine the next slice, this can simply be our change in x between the slices. Change in x is always represented as dx. So we can simply say the height of each cylinder is

$$h=dx.$$

If we were instead rotating our function around a vertical line (like x=0) the height of our disks would be dy. This is only if we are using the disk method and would not necessarily be the case when using the shell method.

Back to the integral

Now we got our height and radius of each disk we get from slicing this figure. Putting this together, we can say that the volume of a single disk can be represented as

$$V=\pi \big( x^2 \big)^2dx.$$

But this of course is just one disk. We need to add up the volume of all of the disks to get the volume of the full figure. This is exactly what the integral accomplishes. Before doing this, remember we are only rotating this function between x=0 and x=2. So these will be the bounds of our integral. Therefore, the volume of our entire figure can be found with the following integral.

$$\int_0^2 \pi \big( x^2 \big)^2dx$$

4. Solve the integral

We made it through the hard part! Now all we need to do is solve this integral and we will have the volume of our figure. First let’s simplify this integral a little, then we can integrate using the power rule and evaluate at the given bounds.

$$\int_0^2 \pi \big( x^2 \big)^2dx$$

$$\pi \int_0^2 x^4 dx$$

$$\pi \Bigg[ \frac{1}{5} x^5 \Bigg]^2_0$$

$$\frac{\pi}{5} \Big[ (2)^5 – (0)^5 \Big]$$

$$\frac{\pi}{5} \Big[ 32 \Big]$$

$$\frac{32 \pi}{5}$$

So we found that the volume of the solid is \frac{32 \pi}{5}! Hopefully this has helped you with the disk method, but if there’s still a topic you’d like to learn about take a look at some of my other lessons and problem solutions about integrals. Once you know and understand the disk method, another good application of integrals to check out would be the washer method. If you can’t find the topic or question you’re looking for just let me know by emailing me at jakesmathlessons@gmail.com!

I also encourage you to join my email list! Just enter your name and email below and I’ll send you my free calculus 1 study guide as a bonus for joining me!